Information about the solar time clock
Have you also wondered why sundials sometimes go a little ahead or behind? Here you will find the answer.
DIRECTLY TO THE SOLAR TIME CLOCK
Digital Solar Time — Equation Clock
Coordinated time zone clock times, as they are widely used today, show a single time for the areas belonging to a time zone. The displayed time is only correct at the location where it is determined and is subject to fluctuations of ±16 minutes compared to the true solar time even there.
Analog sundials do show the true solar time, but they are dependent on sunlight and must also be permanently installed or aligned with the celestial meridian. Handy analog ring sundials do show the true solar time, but only when the sun is shining and only inaccurately at noon and not at all at the solstices. In addition, it must be known whether it is morning or afternoon.
The fluctuations in the true solar time are caused by the movements of the celestial bodies and their mutual influences therein. The so-called "Equation of time" is a mathematical formula which calculates these fluctuations. The equation of time is the difference between the averaged solar time and the true solar time. A digital sundial with equation of time uses Universal Coordinated Time (UTC+0, or Greenwich Mean Time (GMT)), a longitude coordinate, and the equation of time to calculate the true solar time for any location on Earth at any time of day.
Solar time / Local time - Railroad time - Zone time
Until the introduction of uniform railroad times, the so-called "local time" applied in every place in the world. The local time of each place was read at a sundial, or at the passage of the sun through the celestial meridian (12:00 noon). With second method the true solar time is determined, which is also called true local time (TLT). The TLT is subject to fluctuations, which are averaged for the period of one year in the mean solar time, which is also called mean local time (MLT). Fixed and immovable sundials display TLT. Some sundials have the differences between TLT and MLT attached for general information.
The different times have their origin in their "time maker". For true solar time, the time maker is the sun itself. For mean solar time, the time maker is a clock referenced to the sun. For the digital equation clock, the time maker is a computer referenced to the sun.
The change from solar time to local time to zone time

Left: A sundial with equation of time table for Central European Time (CET) in the Polish city of Jędrzejów. (Photo: Jakub Hałun, CC BY-SA 3.0).
"NALEZY ODJAC MINUT" (You should subtract the minutes [for CET]).
"PIERWSZEGO" (at the first).
"DZIESIATEGO" (on the tenth).
"DWUDZIESTEGO" (on the twentieth).
Middle: Historical indication of the time difference from mean local time to Berlin time at Beverungen station (North Rhine-Westphalia). (Photo: Martin Hasselblatt, CC BY-SA 3.0).
Right: Map of 1894 showing the time zone of Central European Time at the meridian of Stargard (15th degree of longitude) ±30 minutes and the overlying parts of the territory. (Draft: G.Lambelet, Verlag v.Schmidt, Francke & Co., Scan: Dr.-Ing. S.Wetzel, public domain).
With the expansion of rail traffic over greater distances, uniform times were needed for the timetables. Until the introduction of Central European Railway Time (C. R. T.) on June 1, 1891, based on time at the 15th meridian of longitude, German railroads used Berlin time and the mean local times of Munich, Stuttgart and Frankfurt or Ludwigshafen to prepare their timetables. Railroads in other countries used mean local time from their main locations. North American railroads introduced railroad time zones as early as 1883. The difference between time zones was 1 hour and had an extension of 15 degrees of longitude. 15 degrees of longitude equals a time difference of exactly 1 hour. These railroad zone times in the railroad time zones were legislated shortly after their introduction as the zone times in the time zones that are still valid today. The Central European Railway Time (C. R. T.) became the Central European Time (CET).
How does the fluctuation of solar time occur?
The moon, earth and sun each rotate around each other. The rotation path (orbit) of the earth around the sun is not uniformly round, but elliptical. In an elliptical orbit, objects approach and move away from each other. This has an effect on the orbital velocity. The pirouette effect comes into play, like a pirouette in figure skating. If the earth approaches the sun, the orbital velocity of the earth is accelerated. If the earth moves away from the sun, the orbital speed of the earth is slowed down.
In addition, the sun moves around the galaxy center of the Milky Way. Thereby the earth is exposed to a similar situation as the moon. If the orbital direction of the earth is in the same orbital direction of the sun, then the earth must be faster than the sun to pass it, consequently it is slower. If the orbital direction of the earth is opposite to the orbital direction of the sun, then the earth can be slower than the sun and let it pass by, consequently it is faster.
Thus, there are at least 2 forces acting on the rotation of the earth which cause the solar time to fluctuate. In the diagram one of these forces is graphically represented.
Rotation of moon, earth and sun
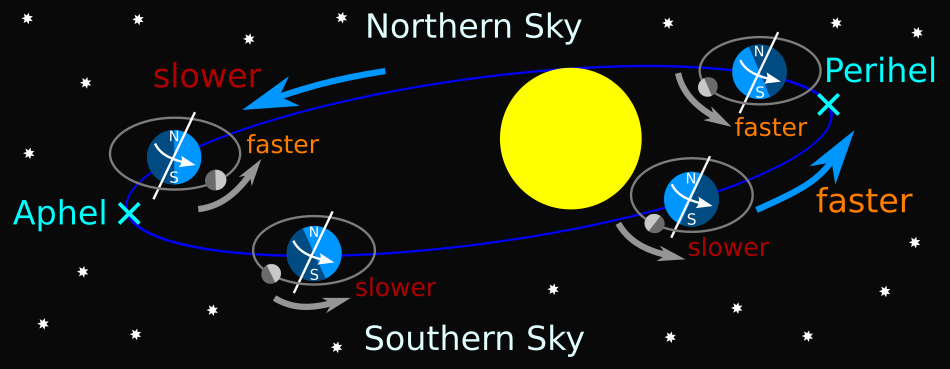
Perihelion: closest point of the earth to the sun — 147 Mio. km — 3. January.
Aphelion: farthest point from the sun on earth — 152 Mio. km — 5. July.
Positions of the Sun compared to local mean time as viewed from the Northern and Southern Hemispheres.
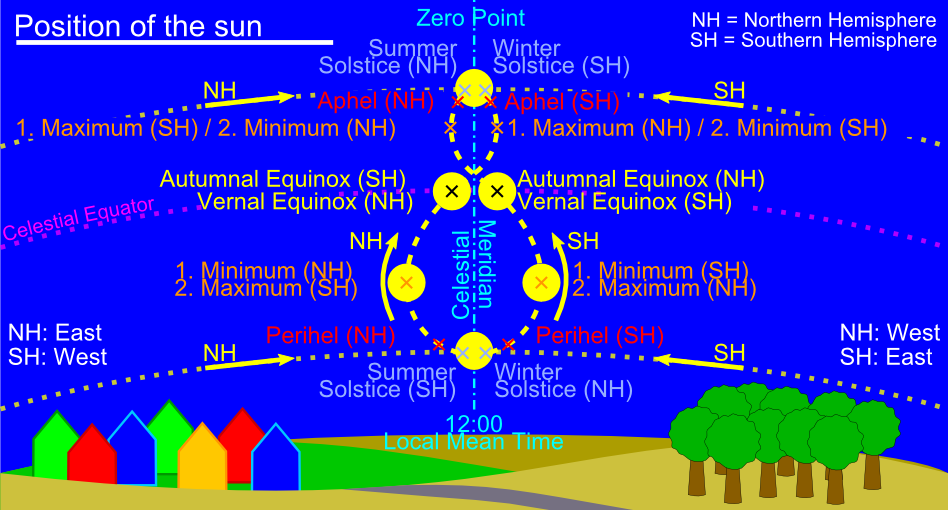
This 8 (analemma) in the sky is created when every day of the year at 12:00 noon in the same place a photo of the sun is taken with a camera fixed to the celestial meridian.
The first solar event at the beginning of the year is a Perihelion.
The penultimate solar event at the end of the year is a solstice.
The last solar event at the end of the year is a zero point.
NH = Northern Hemisphere
SH = Southern Hemisphere
Celestial Meridian
Celestial Equator
Vernal Equinox = Spring Point
Autumnal Equinox = Autumn Point
Summer Solstice
Winter Solstice
Minimum / Maximum = Solar time solstice
Perihelion: closest point to the sun (147 Mio. km)
Aphelion: farthest point from the sun (152 Mio. km)
Local Mean Time
"Zero Point" means that the true solar time coincides with the mean solar time. (TST = MST).
"Minimum Point" means that the true solar time (TST) is in the minus to the mean solar time (MST), thus the sundial goes after. For example, if it is 12:00 MSZ, then it is only 11:44 TST. (TST < MST).
"Maximum Point" means that the true solar time (TST) is in the plus to the mean solar time (MST), thus the sundial goes ahead. If it is 12:00 MSZ, then it is already 12:14 TST, for example. (TST > MST).
The solar cycle of a year:
Perihelion: ~3. January (closest point to the sun, 147 Mio. km)
1. (Greatest) Minimum Point: 11. February (great solar time solstice east, greatest lag of the sun)
Vernal Equinox: 19./20./21. March (Vernal Point (NH) / Autumn Point (SH))
1. Zero Point: 15. April (Simultaneity of time at the zone time determination longitude)
1. (Second Greatest) Maximum Point: 14. May (small solar time solstice west, second greatest lead of the sun)
2. Zero Point: 13. June (Simultaneity of time at the zone time determination longitude)
Summer(NH)/Winter(SH) Solstice: 20./21./22. June (Summer Solstice (NH) / Winter Solstice (SH))
Aphelion: ~5. July (farthest point from the sun, 152 Mio. km)
2. (Second Greatest) Minimum Point: 26 July (small solar time solstice east, second largest lag of the sun)
3. Zero Point: 1. September (Simultaneity of time at the zone time determination longitude)
Autumnal Equinox: 22./23./24. September (Vernal Point (NH) / Autumn Point (SH))
2. (Greatest) Maximum Point: 3. November (great solar time solstice west, greatest lead of the sun)
Winter(NH)/Summer(SH) Solstice: 20./21. December (Winter Solstice (NH) / Summer Solstice (SH))
4. Zero Point: 25. December (Simultaneity of time at the zone time determination longitude)
Positions of the Sun compared to local mean time as viewed from the Northern Hemisphere.
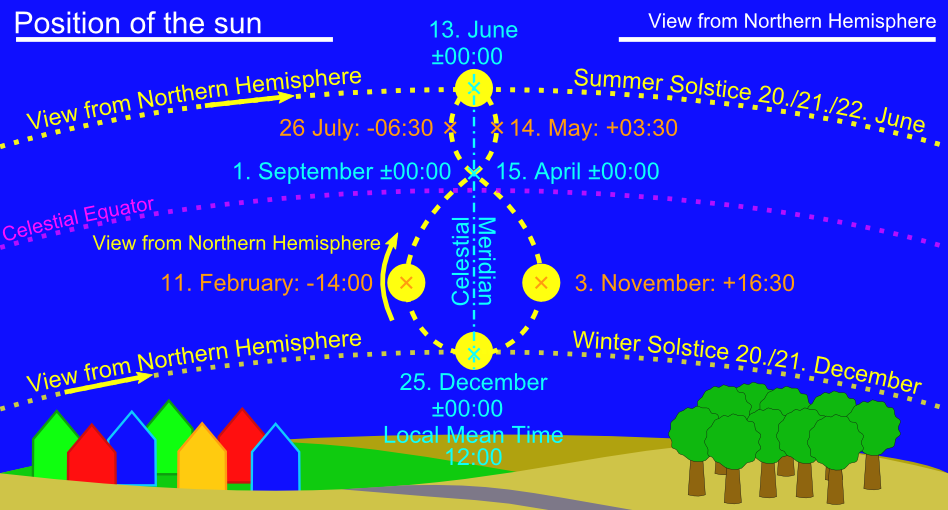
This 8 (analemma) in the sky is created when every day of the year at 12:00 noon CET a photo of the sun is taken with a camera fixed to the celestial meridian.
Example
Zero Point
GMT/London
Difference equation of time: ±00:00
Northwestspain/Santiago de Compostela
Difference to GMT: -36:30
Difference equation of time: ±00:00
11. February (Greatest Minimum Point, Greatest lag of the sun)
GMT/London
Difference equation of time: -14:00
Northwestspain/Santiago de Compostela
Difference to GMT: -50:30 (-36:30 + -14:00 = -50:30)
Difference equation of time: -14:00 (-50:30 - -36:30 = -14:00)
14. May (Second Greatest Maximum Point, Second largest lead of the sun)
GMT/London
Difference equation of time: +03:30
Northwestspain/Santiago de Compostela
Difference to GMT: -33:00 (-36:30 + +03:30 = -33:00)
Difference equation of time: +03:30 (-33:00 - -36:30 = +03:30)
26 July (Second Greatest Minimum Point,Second largest lag of the sun)
GMT/London
Difference equation of time: -06:30
Northwestspain/Santiago de Compostela
Difference to GMT: -43:00 (-36:30 + -06:30 = -43:00)
Difference equation of time: -06:30 (-43:00 - -36:30 = -06:30)
3. November (Greatest Maximum Point, Largest lead of the sun)
GMT/London
Difference equation of time: +16:30
Northwestspain/Santiago de Compostela
Difference to GMT: -20:00 (-36:30 + +16:30 = -20:00)
Difference equation of time: +16:30 (-20:00 - -36:30 = +16:30)
Acceleration and deceleration
The elliptical orbit of the Earth around the Sun (Earth's orbit) is approximately 940,000,000 km (940 million km). The earth orbits the sun in one year. The speed of the earth (earth speed) amounts to 29.77 km/s (107,155.00 km/h) on the average. If the earth approaches the sun on its elliptical orbit around the sun (perihelion), then it is accelerated in its speed on its orbit. If the earth moves away from the sun towards aphelion, then it is decelerated in its velocity on its orbit around the sun. Both have effects on the intrinsic rotation of the earth, by which the length of a day is determined. Due to the elliptical orbit of the earth around the sun, the days in a year are not only shorter or longer, but also become successively slower or faster shorter or longer.
The acceleration and the braking (deceleration) of the velocity of the earth around the sun and consequently also the intrinsic rotation of the earth happens with an accelerated or decelerated deceleration as well as a decelerated or accelerated acceleration.
On January 3 the earth is closest to the sun (perihelion). Already from November 3 an accelerated deceleration of the Earth's proper rotation takes place, which reaches its highest accelerated deceleration two days before the perihelion on January 1. Already 2 days before reaching the perihelion the continuing deceleration is delayed again until the solar equinox on February 11. From February 11, an accelerated deceleration takes place and continues until March 26, when it reaches its highest accelerated deceleration in this phase. From March 26, a decelerated acceleration takes place, reaching its lowest acceleration at the solar equinox on May 14. An accelerated deceleration occurs from May 14 and continues until 13 days before the aphelion on July 5 until June 20, when it reaches its highest deceleration in this phase. From June 20, a delayed deceleration occurs that lasts until 21 days after aphelion on July 5 until the solar equinox on July 26. From July 26, the delayed deceleration changes to an accelerated acceleration and lasts until September 17. From September 17, a delayed acceleration takes place until the solar equinox on November 3. From November 3, an accelerated deceleration takes place until two days before the perihelion on January 3 until January 1, when it reaches its maximum deceleration and then changes back to a decelerated deceleration.
1. January (Perihelion -2 days) to 11. February (solar time solstice): decelerated deceleration.
11. February (solar time solstice) to 26. March: accelerated acceleration.
26. March to 14. May (solar time solstice): decelerated acceleration.
14. May (solar time solstice) to 20. Juny (Aphelion -13 days): accelerated deceleration.
20. Juny (Aphelion -13 days) to 26. July (solar time solstice): decelerated deceleration.
26. July (solar time solstice) to 17. September: accelerated acceleration.
17. September to 3. November (solar time solstice): decelerated acceleration.
3. November (solar time solstice) to 1. January (Perihelion -2 days): accelerated deceleration.
1. January: highest deceleration, +31.52 seconds/day, 1 day = 24:00:31.52 (HH:MM:SS).
11. February: 1 day = 24:00:00 (HH:MM:SS).
26. March: second highest acceleration, -18,17 seconds/day, 1 day = 23:59:41.83 (HH:MM:SS).
14. May: 1 day = 24:00:00 (HH:MM:SS).
20. Juny: second highest deceleration, +13,10 seconds/day, 1 day = 24:00:13.10 (HH:MM:SS).
26. July: 1 day = 24:00:00 (HH:MM:SS).
17. September: highest acceleration, -21,39 seconds/day, 1 day = 23:59:21.39 (HH:MM:SS).
3. November: 1 day = 24:00:00 (HH:MM:SS).
The longest day of the year is January 1 with 24:00:31.52 (HH:MM:SS).
The shortest day of the year is September 17 with 23:59:21.39 (HH:MM:SS).
The earth turns slower and the days are longer:
From 3. November to 11. February.
From 14. May to 26. July.
The earth is spinning faster and the days are shorter:
From 11. February to 14. May.
From 26. July to 3. November.
From November 3 to February 11 (100 days) a total time difference of minus 30 minutes and 30 seconds (-00:30:30, HH:MM:SS) is achieved. Between Christmas and New Year's Day, the Earth rotates ~30 seconds slower each day - one day has 24:00:30 (HH:MM:SS).
Periods of the speed of self-rotation of the Earth on its orbit around the Sun.
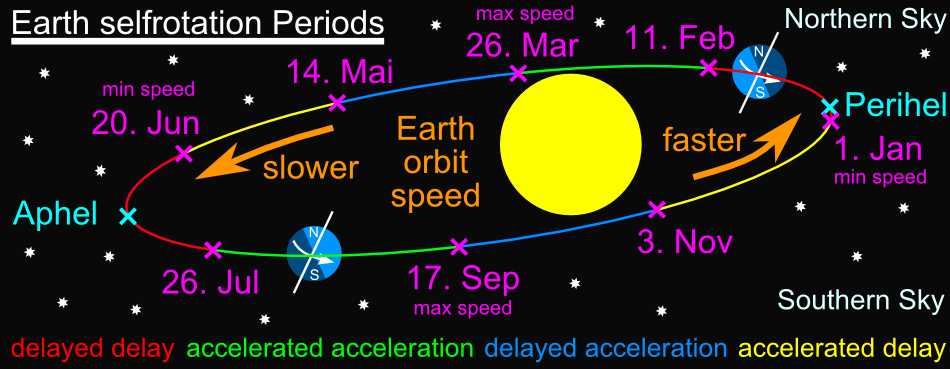
Acceleration periods:
1. January to 26. March: Acceleration.
26. March to 20. Juny: Deceleration.
20. Juny to 17. September: Acceleration.
17. September to 1. January: Deceleration.
3. January: Perihelion - closest point to the sun on earth.
1. January to 11. February: decelerated Deceleration (41 days).
11. February to 26. March: accelerated Acceleration (43 days).
26. March to 14. May: decelerated Acceleration (49 days).
14. May to 20. Juny: accelerated Deceleration (37 days).
5. July: Aphelion - farthest point from the sun on earth.
20. Juny to 26. July: decelerated Deceleration (36 days).
26. July to 17. September: accelerated Acceleration (53 days).
17. September to 3. November: decelerated Acceleration (47 days).
3. November to 1. Januar: accelerated Deceleration (59 days).
3. Januar: Perihelion - closest point to the sun on earth.
Acceleration - Deceleration Periods:
3. Januar to 5. July: 183 days.
20. Juny to 1. Januar: 195 days.
Perihelion - Aphelion Periods:
1. Januar to 20. Juny: 170 days.
5. July to 3. Januar: 182 days.
1. Januar: greatest Periods-Deceleration (24:00:31,52).
3. Januar: Perihelion - closest point to the sun on earth.
1. Januar to 11. Februar: decelerated Deceleration (41 days).
11. Februar: Middle (24:00:00,00).
11. Februar to 26. March: accelerated Acceleration (43 days).
26. March: greatest Periods-Acceleration (23:59:41,83).
26. March to 14. May: decelerated Acceleration (49 days).
14. May: Middle (24:00:00).
14. May to 20. Juny: accelerated Deceleration (37 days).
20. Juny: greatest Periods-Deceleration (24:00:13,10).
5. July: Aphelion - farthest point from the sun on earth.
20. Juny to 26. July: decelerated Deceleration (36 days).
26. July: Middle (24:00:00).
26. July to 17. September: accelerated Acceleration (53 days).
17. September: greatest Periods-Acceleration (23:59:38,61).
17. September to 3. November: decelerated Acceleration (47 days).
3. November: Middle (24:00:00).
3. November to 1. Januar: accelerated Deceleration (59 days).
1. Januar: greatest Periods-Deceleration (24:00:31,52).
3. Januar: Perihelion - closest point to the sun on earth.
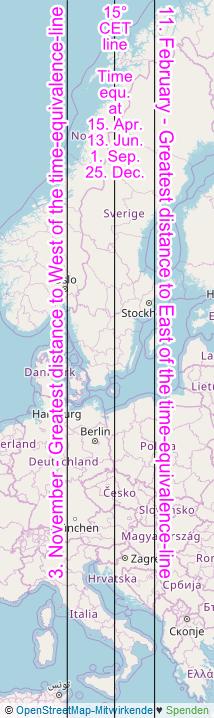
Time Zones Equal Time Line
Every year on April 15, June 13, September 1, and November 3, the solar time at the longitude of a time zone coincides with that zone time (excluding daylight saving time). This coincidence of the two times is called time-equivalence, while the calculation of the time difference between zone time and solar time is called equation of time. With daylight saving time of +1 hour, this time equivalence is shifted 15 degrees of longitude to the east.
The time-equivalence runs along a longitude and can be called time-equivalence-line. The time-equivalence-line shifts outside the time-equivalence-days at the time zone longitude from this to the east or west. The respective longitude of a time zone lies thereby between the largest and smallest distances of the time-equivalence-line to the longitude of a time zone. The distance from the longitude of a time zone to the farthest distance of the equation of time line to the east (on February 11) is smaller than that to the west (on November 3).
From November 3 to February 11, the Equal Time line moves from west to east, passing through the longitude of a time zone on December 25.
From February 11 to May 14, the Equal Time line travels from east to west, passing through the longitude of a time zone on April 15.
From May 14 to July 26, the Equal Time line moves from west to east, passing through the longitude of a time zone on July 13.
From July 26 to November 3, the Equal Time line moves from east to west, passing through the longitude of a time zone on September 1.
The line of simultaneity moves up to ~10 km per day to the east or west. Thus, the line of simultaneity reaches every day other places within the zone in which the line of simultaneity moves from east to west and west to east.
Sunrise and sunset
The sunrises and the sunsets are based not only on the true solar time but also on the maximum daily solar altitude (culmination) above the horizon. The maximum daily solar altitude (culmination) above the horizon is different every day in the periods between the solstices. The angle of elevation of the sun is subject to an annual variation of 46.8°. At the equinoxes the elevation angle of the sun's altitude at the equator is exactly 90°. At this time the ecliptic plane of the earth intersects the equatorial plane of the earth at the celestial meridian. Both planes are offset from each other by 23.4°. The elevation angle of the sun's altitude moves 46.8° toward or away from the horizon between the two solstices and passes through the halfway point of 23.4° at the equinoxes.
From 20/21/22 June (summer solstice) to 20/21 December (winter solstice) the maximum daily solar altitude moves towards the horizon and from 20/21 December (winter solstice) to 20/21/22 June (summer solstice) it moves away from the horizon.
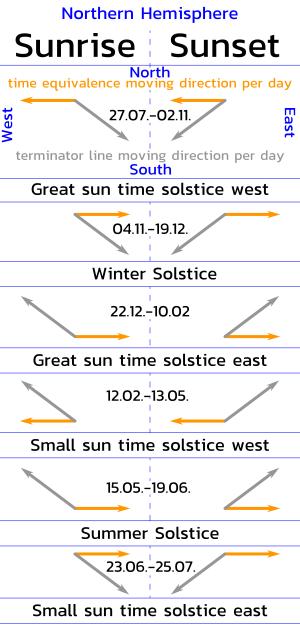
The interaction of the fluctuations of true solar time and the daily changing solar maximum (culmination) results in the fact that the temporal shift of the day-and-night-boundary (terminator) is sometimes faster and sometimes slower from day to day. This is most noticeable between the date of the Sun's Greatest Advance on November 3 and the date of the Winter Solstice on December 20/21. Between November 04 and December 04 (30 days) the sunrise shifts by 48 minutes, while the sunset shifts by only 35 minutes in the same period. Exactly the opposite is the case in the period between the winter solstice on 20/21 December and the sun's greatest postlapse on 11 February. Between January 11 and February 10 (30 days) the sunrise shifts by only 39 minutes, while the sunset shifts by 51 minutes in the same period.
The differences change at each solstice and each solar time solstice. Solstices are two per year and solar time solstices are four per year - two minor solar time solstices and two major solar time solstices.
11. February: Great solar time solstice east ( greatest lag of the sun)
14. May: Small solar time solstice west (second largest lead of the sun)
26. July: Small solar time solstice east (second largest solar lag)
03. November: Great solar time solstice west ( greatest lead of the sun)
Side info: The light of the sun needs 8 minutes and 19 seconds (499 seconds) on its way to the earth.
So the sun is never there in the sky where it can be seen, but already 8 minutes and 19 seconds (499 seconds) further.
Conventional mechanical and digital clocks always show only an average local time, which deviates from the true solar time. With these clocks, each second, minute and hour in a day is always the same length. With the true solar time, the length of a second, minute and hour in a day varies, because the celestial bodies influence each other in their movement. With analog sundials, the true solar time and thus the difference to the mean local time is indicated by the sun itself, but only when the sun is shining. With digital sundials, the variations are compensated by a so-called "equation of time". The equation of time is a mathematical calculation of the difference between local mean time and local apparent time. Digital sundials display the true solar time at all times.
Equatorial sundial "Bernhardt's roller" - Mean solar time

Left: Equatorial sundial "Bernhardt's roller" with a summer roller at the Planetarium Stuttgart.
Middle: Equatorial sundial "Bernhardt's roller" with a winter roller at the Planetarium Stuttgart.
Right: Equatorial sundial "Bernhardt's roller" with a winter roller at the Planetarium Stuttgart and drawing of a simple equatorial sundial.
Photos: Stefan-Xp, CC BY SA 3.0; Draft: public domain.
An equatorial sundial is aligned with the equator and the Earth's axis. With an equatorial sundial with "Bernhardt's rollers", the mean solar time can be displayed. An equatorial sundial with "Bernhardt's rollers" takes advantage of the natural fact that shadows are longer in winter and shorter in summer. In a simple equatorial sundial, the dial is a disc and is parallel to the earth's equatorial plane. The hand (shadow caster) is parallel to the Earth's axis. In an equatorial sundial with a "Bernhardt's roller" as shadow hand (gnomon), the celestial anemma of the sun is balanced by the conical rollers and the mean solar time is displayed at the front shadow edge. For the equation of time, two Bernhardt rollers are needed - a summer roller and a winter roller - which have to be exchanged at the zero points on June 13 and December 25, because the sun-sky analemma is not symmetrical. If the analemma were symmetrical, the roller would only have to be turned over at these two zero points. In a disk dial, the upper or lower disk is illuminated by the sun, depending on the position of the sun. This is especially clear if the location is on the equator. If the location is closer to the Earth's poles, a disk shaped into a funnel can compensate for the change from top to bottom (see photos).
The solar time
The true solar time is the time calculated on a day according to the highest position of the sun. If the sun is at the celestial meridian, i.e. at its highest, then it is 12:00 noon there. A distinction is made between "true solar time" (true local time, TLT) and "mean solar time" (mean local time, MLT). The mean solar time can deviate up to 16 minutes from the true solar time. The reason for this is the uneven speed of the earth on its elliptical orbit and the inclination of the earth's axis. Mean solar time compensates for the variations in true solar time by averaging out over the year. Greenwich Mean Time (GMT) is a mean solar time.
The true solar time
For the analogous calculation of the true solar time for a day, the time must be noted at a location at which the sun is at its highest point, or passes through the celestial meridian. The time difference between this time and the 12:00 noon local mean time changes over the course of a year. The time difference, or variation within a year, can be observed in the sky as analemma (8).
The digital solar time
The digital solar time is calculated from the Greenwich Mean Time (GMT), or UTC+0, the equation of time and the geographical longitude. The position of a place on the earth can be determined by the geographical longitude and latitude. The television tower on Alexanderplatz in Berlin (Germany) is located at 52.520817° northern latitude and 13.409414° eastern longitude. The longitude is needed to calculate the digital solar time.
Greenwich Mean Time (GMT)
Greenwich Mean Time (GMT) is the mean solar time at the prime meridian (0°) in London, England. Coordinated Universal Time (UTC) is based on Greenwich Mean Time (GMT). Universal Time (UT), on the other hand, is based on true solar time.
Universal Time Coordinated (UTC)
The time in the worldwide time zones, such as Central European Time (CET), which is valid in Central European countries, is coordinated with Greenwich Mean Time (GMT). The initial time for all time zones is called "Coordinated Universal Time" (UTC; English: Coordinated Universal Time; French: Temps universel coordonné).
The 24 time zones on Earth shown on a map.

Graphic: CIA & solar-time.org, public domain.
Time zones and zone time
The Earth is divided into 24 time zones with different zone times. A zone time (English zone time, standard time) is the uniform time in a time zone. The basis of a zone time is the coordinated universal time (UTC) and a longitude of the earth. Central European Time (CET) is aligned with the 15th degree of longitude east (15°E). CET at the 15th meridian of longitude east is exactly one hour from UTC at the prime meridian (0°). Coordinated Universal Time (UTC) is given as UTC+0 for Greenwich Mean Time (GMT) and UTC+1 for Central European Time (CET).
The time zones in Europe shown in a map.
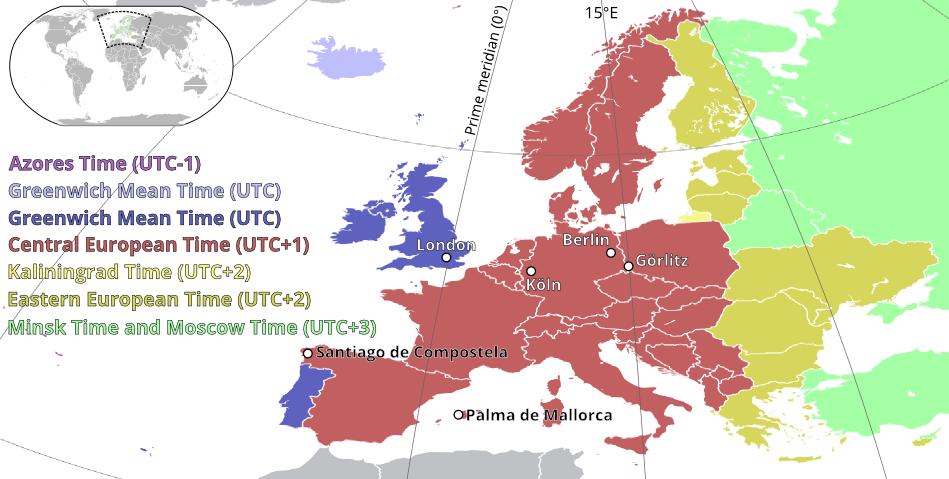
Raw graphic: Rob984 wikimedia (CC BY-SA 4.0)
Criticism of Central European Summer Time (CEST)
The most widespread criticism of Central European Summer Time (CEST) is that, compared to Central European Time (CET), the time in CEST is actually set back one hour, with respect to the fact that people with regular working hours have to go to bed one hour earlier in the evening and get up one hour earlier in the morning. Those who have to go to bed at 23:00 CET and get up at 06:00 in order to get to work rested and on time, have to go to bed at 22:00 CET and get up at 05:00 CET. Of course, in summer it is partly still light at 22:00 and still dark at 05:00, which has an impact on sleep.
For all appointments in CEST, they are always one hour earlier according to CET. You have an appointment at 07:00 in CEST? Then you have the appointment at 06:00 according to CET.
The introduction of CEST had purely economic interests in the European internal market. Health aspects were not taken into account. A time change and the associated shift in bedtime has a negative impact on health. This in turn leads to higher costs for health care and consequently to an economic strengthening of the pharmaceutical industry. Already at the time of the introduction of CEST in Europe (1973 to 1981) Donald Rumsfeld (1975-1977 Secretary of Defense of the USA, 1977-1985 Chairman of the Board of G.D. Searle & Company (introduction of aspartame, from 1985 Monsanto)) warned of the change of danger from the military-industrial complex to the danger from the pharmaceutical-industrial complex. Changes in bedtime mean stress for body and soul and can lead to depression and cancer, where the numbers of people affected are steadily increasing.
Midday sun shift
The digital solar time looks like a gimmick at first glance. But it can also be helpful. In the summer months, some people are advised to avoid the midday sun. Now, Central European Time (CET) deviates very far from true solar time in some locations. Thus, at locations in Germany alone, the midday sun can deviate by up to 1 hour compared to CET.
New Year's Eve & Midnight
The advantage of the digital sundial is that it works even without the sun. Thus, the digital sundial also shows the exact time of midnight. Celebrating the turn of the year on New Year's Eve is possible with the digital sundial in any place in the world according to true solar time (±30 seconds).
Examples:
Central European Time (CET) is 00:06:22 (6 minutes and 22 seconds) different from local mean time at the TV Tower at Alexanderplatz in Berlin. At the TV Tower on Alexanderplatz in Berlin (Germany), midnight (00:00:00) is only 6 minutes and 22 seconds later than CET. Added to this is the difference from true solar time, which fluctuates over a solar year.
At Cologne Cathedral (Germany), Central European Time (CET) differs from local mean time by 00:32:10 (32 minutes and 10 seconds). At Cologne Cathedral, according to mean local time, midnight (00:00:00) is only 32 minutes and 10 seconds later than according to CET. Added to this is the difference from true solar time, which fluctuates over a solar year.
At the beach of Palma de Mallorca (Spain), the Central European Time (CET) differs from the local mean time by 00:49:21 (49 minutes and 21 seconds). At the beach of Palma de Mallorca (Spain), midnight (00:00:00) is 49 minutes and 21 seconds later than CET. Added to this is the difference from true solar time, which fluctuates over a solar year.
The city of Santiago de Compostela in Galicia (Spain) is located west of the prime meridian, i.e. west of Greenwich Mean Time (GMT), but it is not GMT that applies there, but CET. Consequently, the difference between CET and mean local time there is greater than that between CET and GMT. At the Cathedral of Santiago de Compostela in Galicia (Spain), the Central European Time (CET) differs from the mean local time by 01:34:10 (1 hour, 34 minutes and 10 seconds). At the Cathedral of Santiago de Compostela in Galicia (Spain), midnight (00:00:00) is only 1 hour, 34 minutes and 10 seconds later than CET. Added to this is the difference from true solar time, which fluctuates over a solar year.

Nordisk familjebok (1918), runeberg.org, public domain
Stonehenge and the true Suntime
Note: The times are time-averaged by a few seconds because of elliptical earth's orbit, so that the correlation is easier to recognize.
Stonehenge at winter solstice
Suntime: GMT - 05:30 minutes
Time-equivalence line (Suntime = GMT) at longitude -0.48° (West)
Stonehenge at summer solstice
Suntime: GMT - 09:10 minutes
Time-equivalence line (Suntime = GMT) at longitude 0.43° (East)
Stonehenge
Suntime difference between winter solstice and summer solstice
Suntime at winter solstice + 03:40 compared to suntime at summer solstice
03:40 / 02 = 01:50 minutes
01:50 * 03 = 05:30 minutes
01:50 * 04 = 07:20 minutes
01:50 * 05 = 09:10 minutes
01:50 * 08 = 14:40 minutes
01:50 * 12 = 22:00 minutes
01:50 * 17 = 31:10 minutes
Greenwich at winter solstice
Suntime: GMT + 01:50 minutes
Greenwich at summer solstice
Suntime: GMT - 01:50 minutes
Difference: 03:40 minutes
Stonehenge at vernal equinox
19./20./21. March
Stonehenge Suntime: GMT - 14:40 minutes
Time-equivalence line (Suntime = GMT) at longitude 1.88° (East)
Stonehenge at autumnal equinox
22./23./24. September
Stonehenge Suntime: GMT + 00:00 = time-equivalence (Suntime = GMT)
Time-equivalence line (Suntime = GMT) at longitude -1.82° (West)
Stonehenge is at longitude -1.82°
Greenwich at vernal equinox
19./20./21. March
Greenwich Suntime: GMT - 07:20 minutes
Greenwich at autumnalequinox
22./23./24. September
Greenwich Suntime: GMT + 07:20 minutes
Stonehenge at time-equivalence (Suntime = GMT) in Greenwich
15. April, 13. June, 1. September, 25. December
Suntime: GMT - 07:20 minutes
Stonehenge at Great sun time solstice east
11. February
Time-equivalence line (Suntime = GMT) at longitude 3.56° (East)
Stonehenge Suntime: GMT - 21:30 minutes (+ 00:30 elliptical orbit adjustment = 22:00)
Stonehenge longitude -1.82° (West)
Stonehenge at Great sun time solstice west
03. November
Time-equivalence line (Suntime = GMT) at longitude -4.11° (West)
Stonehenge Suntime: GMT + 09:10 minutes
Stonehenge longitude -1.82° (West)
Stonehenge
Suntime difference between 11. February and 3. November
21:30 + 09:10 = 30:40 minutes (+ 00:30 elliptical orbit adjustment = 31:10)
Stonehenge at Small sun time solstice west
14. May
Time-equivalence line (Suntime = GMT) at longitude -0.92° (West)
Stonehenge Suntime: GMT - 03:40 minutes
Stonehenge longitude -1.82° (West)
Stonehenge at Small sun time solstice east
26. July
Time-equivalence line (Suntime = GMT) at longitude 1.63° (East)
Stonehenge Suntime: GMT - 13:50 minutes
Stonehenge longitude -1.82° (West)
On May 14th, Stonehenge is about twice as far from Greenwich Prime Meridian as the Small sun time solstice west time-equivalence line (local suntime = GMT). The Greenwich Prime Meridian is at the longitude 0°. The time-equivalence line is on May 14th at the longitude -0.91°. Stonehenge is at the longitude -1.82°.
In Stonehenge the time difference between the solstices is 03:40 minutes. Half of it is 01:50 minutes, the double is 07:20 minutes and the quadruple is 14:40 minutes. In Greenwich, at the solstice days, the time difference between local solar time and GMT is 01:50 minutes. In Greenwich, on the day of equinoxes, the time difference between local solar time and GMT is 07:20 minutes. The double is 14:40 minutes. In Stonehenge, on the day of vernal equinox, the time difference between local solar time and GMT is 14:40 minutes. In Stonehenge, on the day of autumnal equinox, the time-equivalence line (Suntime = GMT) is at Stonehenge.
SOLAR TIME CLOCK
DIRECTLY TO THE SOLAR TIME CLOCK
Digital Solar Time — Equation Clock
Coordinated time zone clock times, as they are widely used today, show a single time for the areas belonging to a time zone. The displayed time is only correct at the location where it is determined and is subject to fluctuations of ±16 minutes compared to the true solar time even there.
Analog sundials do show the true solar time, but they are dependent on sunlight and must also be permanently installed or aligned with the celestial meridian. Handy analog ring sundials do show the true solar time, but only when the sun is shining and only inaccurately at noon and not at all at the solstices. In addition, it must be known whether it is morning or afternoon.
The fluctuations in the true solar time are caused by the movements of the celestial bodies and their mutual influences therein. The so-called "Equation of time" is a mathematical formula which calculates these fluctuations. The equation of time is the difference between the averaged solar time and the true solar time. A digital sundial with equation of time uses Universal Coordinated Time (UTC+0, or Greenwich Mean Time (GMT)), a longitude coordinate, and the equation of time to calculate the true solar time for any location on Earth at any time of day.
Solar time / Local time - Railroad time - Zone time
Until the introduction of uniform railroad times, the so-called "local time" applied in every place in the world. The local time of each place was read at a sundial, or at the passage of the sun through the celestial meridian (12:00 noon). With second method the true solar time is determined, which is also called true local time (TLT). The TLT is subject to fluctuations, which are averaged for the period of one year in the mean solar time, which is also called mean local time (MLT). Fixed and immovable sundials display TLT. Some sundials have the differences between TLT and MLT attached for general information.
The different times have their origin in their "time maker". For true solar time, the time maker is the sun itself. For mean solar time, the time maker is a clock referenced to the sun. For the digital equation clock, the time maker is a computer referenced to the sun.
The change from solar time to local time to zone time

Left: A sundial with equation of time table for Central European Time (CET) in the Polish city of Jędrzejów. (Photo: Jakub Hałun, CC BY-SA 3.0).
"NALEZY ODJAC MINUT" (You should subtract the minutes [for CET]).
"PIERWSZEGO" (at the first).
"DZIESIATEGO" (on the tenth).
"DWUDZIESTEGO" (on the twentieth).
Middle: Historical indication of the time difference from mean local time to Berlin time at Beverungen station (North Rhine-Westphalia). (Photo: Martin Hasselblatt, CC BY-SA 3.0).
Right: Map of 1894 showing the time zone of Central European Time at the meridian of Stargard (15th degree of longitude) ±30 minutes and the overlying parts of the territory. (Draft: G.Lambelet, Verlag v.Schmidt, Francke & Co., Scan: Dr.-Ing. S.Wetzel, public domain).
With the expansion of rail traffic over greater distances, uniform times were needed for the timetables. Until the introduction of Central European Railway Time (C. R. T.) on June 1, 1891, based on time at the 15th meridian of longitude, German railroads used Berlin time and the mean local times of Munich, Stuttgart and Frankfurt or Ludwigshafen to prepare their timetables. Railroads in other countries used mean local time from their main locations. North American railroads introduced railroad time zones as early as 1883. The difference between time zones was 1 hour and had an extension of 15 degrees of longitude. 15 degrees of longitude equals a time difference of exactly 1 hour. These railroad zone times in the railroad time zones were legislated shortly after their introduction as the zone times in the time zones that are still valid today. The Central European Railway Time (C. R. T.) became the Central European Time (CET).
How does the fluctuation of solar time occur?
The moon, earth and sun each rotate around each other. The rotation path (orbit) of the earth around the sun is not uniformly round, but elliptical. In an elliptical orbit, objects approach and move away from each other. This has an effect on the orbital velocity. The pirouette effect comes into play, like a pirouette in figure skating. If the earth approaches the sun, the orbital velocity of the earth is accelerated. If the earth moves away from the sun, the orbital speed of the earth is slowed down.
In addition, the sun moves around the galaxy center of the Milky Way. Thereby the earth is exposed to a similar situation as the moon. If the orbital direction of the earth is in the same orbital direction of the sun, then the earth must be faster than the sun to pass it, consequently it is slower. If the orbital direction of the earth is opposite to the orbital direction of the sun, then the earth can be slower than the sun and let it pass by, consequently it is faster.
Thus, there are at least 2 forces acting on the rotation of the earth which cause the solar time to fluctuate. In the diagram one of these forces is graphically represented.
Rotation of moon, earth and sun

Perihelion: closest point of the earth to the sun — 147 Mio. km — 3. January.
Aphelion: farthest point from the sun on earth — 152 Mio. km — 5. July.
Positions of the Sun compared to local mean time as viewed from the Northern and Southern Hemispheres.

This 8 (analemma) in the sky is created when every day of the year at 12:00 noon in the same place a photo of the sun is taken with a camera fixed to the celestial meridian.
The first solar event at the beginning of the year is a Perihelion.
The penultimate solar event at the end of the year is a solstice.
The last solar event at the end of the year is a zero point.
NH = Northern Hemisphere
SH = Southern Hemisphere
Celestial Meridian
Celestial Equator
Vernal Equinox = Spring Point
Autumnal Equinox = Autumn Point
Summer Solstice
Winter Solstice
Minimum / Maximum = Solar time solstice
Perihelion: closest point to the sun (147 Mio. km)
Aphelion: farthest point from the sun (152 Mio. km)
Local Mean Time
"Zero Point" means that the true solar time coincides with the mean solar time. (TST = MST).
"Minimum Point" means that the true solar time (TST) is in the minus to the mean solar time (MST), thus the sundial goes after. For example, if it is 12:00 MSZ, then it is only 11:44 TST. (TST < MST).
"Maximum Point" means that the true solar time (TST) is in the plus to the mean solar time (MST), thus the sundial goes ahead. If it is 12:00 MSZ, then it is already 12:14 TST, for example. (TST > MST).
The solar cycle of a year:
Perihelion: ~3. January (closest point to the sun, 147 Mio. km)
1. (Greatest) Minimum Point: 11. February (great solar time solstice east, greatest lag of the sun)
Vernal Equinox: 19./20./21. March (Vernal Point (NH) / Autumn Point (SH))
1. Zero Point: 15. April (Simultaneity of time at the zone time determination longitude)
1. (Second Greatest) Maximum Point: 14. May (small solar time solstice west, second greatest lead of the sun)
2. Zero Point: 13. June (Simultaneity of time at the zone time determination longitude)
Summer(NH)/Winter(SH) Solstice: 20./21./22. June (Summer Solstice (NH) / Winter Solstice (SH))
Aphelion: ~5. July (farthest point from the sun, 152 Mio. km)
2. (Second Greatest) Minimum Point: 26 July (small solar time solstice east, second largest lag of the sun)
3. Zero Point: 1. September (Simultaneity of time at the zone time determination longitude)
Autumnal Equinox: 22./23./24. September (Vernal Point (NH) / Autumn Point (SH))
2. (Greatest) Maximum Point: 3. November (great solar time solstice west, greatest lead of the sun)
Winter(NH)/Summer(SH) Solstice: 20./21. December (Winter Solstice (NH) / Summer Solstice (SH))
4. Zero Point: 25. December (Simultaneity of time at the zone time determination longitude)
Positions of the Sun compared to local mean time as viewed from the Northern Hemisphere.

This 8 (analemma) in the sky is created when every day of the year at 12:00 noon CET a photo of the sun is taken with a camera fixed to the celestial meridian.
Example
Zero Point
GMT/London
Difference equation of time: ±00:00
Northwestspain/Santiago de Compostela
Difference to GMT: -36:30
Difference equation of time: ±00:00
11. February (Greatest Minimum Point, Greatest lag of the sun)
GMT/London
Difference equation of time: -14:00
Northwestspain/Santiago de Compostela
Difference to GMT: -50:30 (-36:30 + -14:00 = -50:30)
Difference equation of time: -14:00 (-50:30 - -36:30 = -14:00)
14. May (Second Greatest Maximum Point, Second largest lead of the sun)
GMT/London
Difference equation of time: +03:30
Northwestspain/Santiago de Compostela
Difference to GMT: -33:00 (-36:30 + +03:30 = -33:00)
Difference equation of time: +03:30 (-33:00 - -36:30 = +03:30)
26 July (Second Greatest Minimum Point,Second largest lag of the sun)
GMT/London
Difference equation of time: -06:30
Northwestspain/Santiago de Compostela
Difference to GMT: -43:00 (-36:30 + -06:30 = -43:00)
Difference equation of time: -06:30 (-43:00 - -36:30 = -06:30)
3. November (Greatest Maximum Point, Largest lead of the sun)
GMT/London
Difference equation of time: +16:30
Northwestspain/Santiago de Compostela
Difference to GMT: -20:00 (-36:30 + +16:30 = -20:00)
Difference equation of time: +16:30 (-20:00 - -36:30 = +16:30)
Acceleration and deceleration
The elliptical orbit of the Earth around the Sun (Earth's orbit) is approximately 940,000,000 km (940 million km). The earth orbits the sun in one year. The speed of the earth (earth speed) amounts to 29.77 km/s (107,155.00 km/h) on the average. If the earth approaches the sun on its elliptical orbit around the sun (perihelion), then it is accelerated in its speed on its orbit. If the earth moves away from the sun towards aphelion, then it is decelerated in its velocity on its orbit around the sun. Both have effects on the intrinsic rotation of the earth, by which the length of a day is determined. Due to the elliptical orbit of the earth around the sun, the days in a year are not only shorter or longer, but also become successively slower or faster shorter or longer.
The acceleration and the braking (deceleration) of the velocity of the earth around the sun and consequently also the intrinsic rotation of the earth happens with an accelerated or decelerated deceleration as well as a decelerated or accelerated acceleration.
On January 3 the earth is closest to the sun (perihelion). Already from November 3 an accelerated deceleration of the Earth's proper rotation takes place, which reaches its highest accelerated deceleration two days before the perihelion on January 1. Already 2 days before reaching the perihelion the continuing deceleration is delayed again until the solar equinox on February 11. From February 11, an accelerated deceleration takes place and continues until March 26, when it reaches its highest accelerated deceleration in this phase. From March 26, a decelerated acceleration takes place, reaching its lowest acceleration at the solar equinox on May 14. An accelerated deceleration occurs from May 14 and continues until 13 days before the aphelion on July 5 until June 20, when it reaches its highest deceleration in this phase. From June 20, a delayed deceleration occurs that lasts until 21 days after aphelion on July 5 until the solar equinox on July 26. From July 26, the delayed deceleration changes to an accelerated acceleration and lasts until September 17. From September 17, a delayed acceleration takes place until the solar equinox on November 3. From November 3, an accelerated deceleration takes place until two days before the perihelion on January 3 until January 1, when it reaches its maximum deceleration and then changes back to a decelerated deceleration.
1. January (Perihelion -2 days) to 11. February (solar time solstice): decelerated deceleration.
11. February (solar time solstice) to 26. March: accelerated acceleration.
26. March to 14. May (solar time solstice): decelerated acceleration.
14. May (solar time solstice) to 20. Juny (Aphelion -13 days): accelerated deceleration.
20. Juny (Aphelion -13 days) to 26. July (solar time solstice): decelerated deceleration.
26. July (solar time solstice) to 17. September: accelerated acceleration.
17. September to 3. November (solar time solstice): decelerated acceleration.
3. November (solar time solstice) to 1. January (Perihelion -2 days): accelerated deceleration.
1. January: highest deceleration, +31.52 seconds/day, 1 day = 24:00:31.52 (HH:MM:SS).
11. February: 1 day = 24:00:00 (HH:MM:SS).
26. March: second highest acceleration, -18,17 seconds/day, 1 day = 23:59:41.83 (HH:MM:SS).
14. May: 1 day = 24:00:00 (HH:MM:SS).
20. Juny: second highest deceleration, +13,10 seconds/day, 1 day = 24:00:13.10 (HH:MM:SS).
26. July: 1 day = 24:00:00 (HH:MM:SS).
17. September: highest acceleration, -21,39 seconds/day, 1 day = 23:59:21.39 (HH:MM:SS).
3. November: 1 day = 24:00:00 (HH:MM:SS).
The longest day of the year is January 1 with 24:00:31.52 (HH:MM:SS).
The shortest day of the year is September 17 with 23:59:21.39 (HH:MM:SS).
The earth turns slower and the days are longer:
From 3. November to 11. February.
From 14. May to 26. July.
The earth is spinning faster and the days are shorter:
From 11. February to 14. May.
From 26. July to 3. November.
From November 3 to February 11 (100 days) a total time difference of minus 30 minutes and 30 seconds (-00:30:30, HH:MM:SS) is achieved. Between Christmas and New Year's Day, the Earth rotates ~30 seconds slower each day - one day has 24:00:30 (HH:MM:SS).
Periods of the speed of self-rotation of the Earth on its orbit around the Sun.

Acceleration periods:
1. January to 26. March: Acceleration.
26. March to 20. Juny: Deceleration.
20. Juny to 17. September: Acceleration.
17. September to 1. January: Deceleration.
3. January: Perihelion - closest point to the sun on earth.
1. January to 11. February: decelerated Deceleration (41 days).
11. February to 26. March: accelerated Acceleration (43 days).
26. March to 14. May: decelerated Acceleration (49 days).
14. May to 20. Juny: accelerated Deceleration (37 days).
5. July: Aphelion - farthest point from the sun on earth.
20. Juny to 26. July: decelerated Deceleration (36 days).
26. July to 17. September: accelerated Acceleration (53 days).
17. September to 3. November: decelerated Acceleration (47 days).
3. November to 1. Januar: accelerated Deceleration (59 days).
3. Januar: Perihelion - closest point to the sun on earth.
Acceleration - Deceleration Periods:
3. Januar to 5. July: 183 days.
20. Juny to 1. Januar: 195 days.
Perihelion - Aphelion Periods:
1. Januar to 20. Juny: 170 days.
5. July to 3. Januar: 182 days.
1. Januar: greatest Periods-Deceleration (24:00:31,52).
3. Januar: Perihelion - closest point to the sun on earth.
1. Januar to 11. Februar: decelerated Deceleration (41 days).
11. Februar: Middle (24:00:00,00).
11. Februar to 26. March: accelerated Acceleration (43 days).
26. March: greatest Periods-Acceleration (23:59:41,83).
26. March to 14. May: decelerated Acceleration (49 days).
14. May: Middle (24:00:00).
14. May to 20. Juny: accelerated Deceleration (37 days).
20. Juny: greatest Periods-Deceleration (24:00:13,10).
5. July: Aphelion - farthest point from the sun on earth.
20. Juny to 26. July: decelerated Deceleration (36 days).
26. July: Middle (24:00:00).
26. July to 17. September: accelerated Acceleration (53 days).
17. September: greatest Periods-Acceleration (23:59:38,61).
17. September to 3. November: decelerated Acceleration (47 days).
3. November: Middle (24:00:00).
3. November to 1. Januar: accelerated Deceleration (59 days).
1. Januar: greatest Periods-Deceleration (24:00:31,52).
3. Januar: Perihelion - closest point to the sun on earth.
Time Zones Equal Time Line
Every year on April 15, June 13, September 1, and November 3, the solar time at the longitude of a time zone coincides with that zone time (excluding daylight saving time). This coincidence of the two times is called time-equivalence, while the calculation of the time difference between zone time and solar time is called equation of time. With daylight saving time of +1 hour, this time equivalence is shifted 15 degrees of longitude to the east.
The time-equivalence runs along a longitude and can be called time-equivalence-line. The time-equivalence-line shifts outside the time-equivalence-days at the time zone longitude from this to the east or west. The respective longitude of a time zone lies thereby between the largest and smallest distances of the time-equivalence-line to the longitude of a time zone. The distance from the longitude of a time zone to the farthest distance of the equation of time line to the east (on February 11) is smaller than that to the west (on November 3).
From November 3 to February 11, the Equal Time line moves from west to east, passing through the longitude of a time zone on December 25.
From February 11 to May 14, the Equal Time line travels from east to west, passing through the longitude of a time zone on April 15.
From May 14 to July 26, the Equal Time line moves from west to east, passing through the longitude of a time zone on July 13.
From July 26 to November 3, the Equal Time line moves from east to west, passing through the longitude of a time zone on September 1.
The line of simultaneity moves up to ~10 km per day to the east or west. Thus, the line of simultaneity reaches every day other places within the zone in which the line of simultaneity moves from east to west and west to east.
Locations that lie on the farthest west line of coincidence on November 3.
Stjordal (near Trondheim, Atlantic)
Oslo Grorud (Skagerrak/North Sea)
Oldenburg in Holstein
Travemünde Priwall (East Sea)
Cronskamp
Middefeitz
Schnega Bahnhof
Wendischhorst near Kleistau
Rappbodetalsperre-Staumauer
Sondershausen Östertal and Jecha
Witterda (near Erfurt)
Apfelstädt and Bittstädt (near Arnstadt)
Talsperre Schönbrunn (Thuringian Forest)
Breitengüßbach
Bamberg
Herzogenaurach
Augsburg
Schongau/Lech
Lermoos and Biberwier (near Ehrwald)
Naturpark Ötztal
Arco (near Lake Garda)
San Pietro in Cariano
Airport Verona
Modena Madonnina
Pontelungo (near Pistoia)
Marcignana (near Empoli)
Castiglione Della Pescia
Isola del Giglio (Mittelmeer)
Stjordal (near Trondheim, Atlantic)
Oslo Grorud (Skagerrak/North Sea)
Oldenburg in Holstein
Travemünde Priwall (East Sea)
Cronskamp
Middefeitz
Schnega Bahnhof
Wendischhorst near Kleistau
Rappbodetalsperre-Staumauer
Sondershausen Östertal and Jecha
Witterda (near Erfurt)
Apfelstädt and Bittstädt (near Arnstadt)
Talsperre Schönbrunn (Thuringian Forest)
Breitengüßbach
Bamberg
Herzogenaurach
Augsburg
Schongau/Lech
Lermoos and Biberwier (near Ehrwald)
Naturpark Ötztal
Arco (near Lake Garda)
San Pietro in Cariano
Airport Verona
Modena Madonnina
Pontelungo (near Pistoia)
Marcignana (near Empoli)
Castiglione Della Pescia
Isola del Giglio (Mittelmeer)

Places that lie on the most easterly equinox line on February 11.
Insel Kvaloya (near Tromso, Atlantic)
Överhörnäs (near Örnsköldsvik, East Sea)
Spersboda
Kopparmora (Värmdölandet, East Sea)
Insel Gotland (East Sea)
Gdynia Orlowo (near Gdansk, East Sea)
Torun Bielany
Wielun
Rybnik-Polnoc
Polomia (near Jastrzebie-Zdroj)
Bytca
Novaky
Rybnik (near Timace)
Hronske Klacany (near Levice)
Nyergesujfalu (Donau)
Obarok near Bicske
Simontornya
Cepin near Osijek
Koritna
Tinja Gornja
Marina Glava
Kalajevo
Oskova
Bjelogorci
Brezovice
Pale
Jahorina
Meljinie (near Herceg Novi, Mediterranean Sea)
Insel Kvaloya (near Tromso, Atlantic)
Överhörnäs (near Örnsköldsvik, East Sea)
Spersboda
Kopparmora (Värmdölandet, East Sea)
Insel Gotland (East Sea)
Gdynia Orlowo (near Gdansk, East Sea)
Torun Bielany
Wielun
Rybnik-Polnoc
Polomia (near Jastrzebie-Zdroj)
Bytca
Novaky
Rybnik (near Timace)
Hronske Klacany (near Levice)
Nyergesujfalu (Donau)
Obarok near Bicske
Simontornya
Cepin near Osijek
Koritna
Tinja Gornja
Marina Glava
Kalajevo
Oskova
Bjelogorci
Brezovice
Pale
Jahorina
Meljinie (near Herceg Novi, Mediterranean Sea)
Sunrise and sunset
The sunrises and the sunsets are based not only on the true solar time but also on the maximum daily solar altitude (culmination) above the horizon. The maximum daily solar altitude (culmination) above the horizon is different every day in the periods between the solstices. The angle of elevation of the sun is subject to an annual variation of 46.8°. At the equinoxes the elevation angle of the sun's altitude at the equator is exactly 90°. At this time the ecliptic plane of the earth intersects the equatorial plane of the earth at the celestial meridian. Both planes are offset from each other by 23.4°. The elevation angle of the sun's altitude moves 46.8° toward or away from the horizon between the two solstices and passes through the halfway point of 23.4° at the equinoxes.
From 20/21/22 June (summer solstice) to 20/21 December (winter solstice) the maximum daily solar altitude moves towards the horizon and from 20/21 December (winter solstice) to 20/21/22 June (summer solstice) it moves away from the horizon.

| Sunrise & Sunset table with times in »UTC« for London. | |||||||
|---|---|---|---|---|---|---|---|
| Date | Difference | Sunrise | Difference | Sunset | Difference | Day | Night |
| 03.10. | 06:05 | 17:32 | 10:27 | 13:33 | |||
| 02.11. | 30 | 06:56 | 00:51 | 16:30 | 01:02 | 09:34 | 14:26 |
| 03.11. | Great sun time solstice west | ||||||
| 04.11. | 07:00 | 16:27 | 09:27 | 14:33 | |||
| 04.12. | 30 | 07:48 | 00:48 | 15:52 | 00:35 | 08:04 | 15:56 |
| 20./21.12. | Solstice | ||||||
| 11.01. | 08:03 | 16:14 | 08:11 | 15:49 | |||
| 10.02. | 30 | 07:24 | 00:39 | 17:05 | 00:51 | 09:41 | 14:19 |
| 11.02. | Great sun time solstice east | ||||||
| 12.02. | 07:21 | 17:09 | 09:48 | 14:12 | |||
| 14.03. | 30 | 06:18 | 01:03 | 18:02 | 00:53 | 11:44 | 12:16 |
| Sunrise & Sunset table with times in »solar time« for London. | |||||||
|---|---|---|---|---|---|---|---|
| Date | Difference | Sunrise | Difference | Sunset | Difference | Day | Night |
| 03.10. | 06:16 | 17:43 | 10:27 | 13:33 | |||
| 02.11. | 30 | 07:12 | 00:56 | 16:47 | 00:56 | 09:34 | 14:26 |
| 03.11. | Great sun time solstice west | ||||||
| 04.11. | 07:16 | 16:43 | 09:27 | 14:33 | |||
| 04.12. | 30 | 07:58 | 00:42 | 16:01 | 00:42 | 08:04 | 15:56 |
| 20./21.12. | Solstice | ||||||
| 11.01. | 07:55 | 16:06 | 08:11 | 15:49 | |||
| 10.02. | 30 | 07:10 | 00:45 | 16:51 | 00:45 | 09:41 | 14:19 |
| 11.02. | Great sun time solstice east | ||||||
| 12.02. | 07:07 | 16:55 | 09:48 | 14:12 | |||
| 14.03. | 30 | 06:09 | 00:58 | 17:53 | 00:58 | 11:44 | 12:16 |
The differences change at each solstice and each solar time solstice. Solstices are two per year and solar time solstices are four per year - two minor solar time solstices and two major solar time solstices.
11. February: Great solar time solstice east ( greatest lag of the sun)
14. May: Small solar time solstice west (second largest lead of the sun)
26. July: Small solar time solstice east (second largest solar lag)
03. November: Great solar time solstice west ( greatest lead of the sun)
Side info: The light of the sun needs 8 minutes and 19 seconds (499 seconds) on its way to the earth.
So the sun is never there in the sky where it can be seen, but already 8 minutes and 19 seconds (499 seconds) further.
Conventional mechanical and digital clocks always show only an average local time, which deviates from the true solar time. With these clocks, each second, minute and hour in a day is always the same length. With the true solar time, the length of a second, minute and hour in a day varies, because the celestial bodies influence each other in their movement. With analog sundials, the true solar time and thus the difference to the mean local time is indicated by the sun itself, but only when the sun is shining. With digital sundials, the variations are compensated by a so-called "equation of time". The equation of time is a mathematical calculation of the difference between local mean time and local apparent time. Digital sundials display the true solar time at all times.
Equatorial sundial "Bernhardt's roller" - Mean solar time

Left: Equatorial sundial "Bernhardt's roller" with a summer roller at the Planetarium Stuttgart.
Middle: Equatorial sundial "Bernhardt's roller" with a winter roller at the Planetarium Stuttgart.
Right: Equatorial sundial "Bernhardt's roller" with a winter roller at the Planetarium Stuttgart and drawing of a simple equatorial sundial.
Photos: Stefan-Xp, CC BY SA 3.0; Draft: public domain.
An equatorial sundial is aligned with the equator and the Earth's axis. With an equatorial sundial with "Bernhardt's rollers", the mean solar time can be displayed. An equatorial sundial with "Bernhardt's rollers" takes advantage of the natural fact that shadows are longer in winter and shorter in summer. In a simple equatorial sundial, the dial is a disc and is parallel to the earth's equatorial plane. The hand (shadow caster) is parallel to the Earth's axis. In an equatorial sundial with a "Bernhardt's roller" as shadow hand (gnomon), the celestial anemma of the sun is balanced by the conical rollers and the mean solar time is displayed at the front shadow edge. For the equation of time, two Bernhardt rollers are needed - a summer roller and a winter roller - which have to be exchanged at the zero points on June 13 and December 25, because the sun-sky analemma is not symmetrical. If the analemma were symmetrical, the roller would only have to be turned over at these two zero points. In a disk dial, the upper or lower disk is illuminated by the sun, depending on the position of the sun. This is especially clear if the location is on the equator. If the location is closer to the Earth's poles, a disk shaped into a funnel can compensate for the change from top to bottom (see photos).
The solar time
The true solar time is the time calculated on a day according to the highest position of the sun. If the sun is at the celestial meridian, i.e. at its highest, then it is 12:00 noon there. A distinction is made between "true solar time" (true local time, TLT) and "mean solar time" (mean local time, MLT). The mean solar time can deviate up to 16 minutes from the true solar time. The reason for this is the uneven speed of the earth on its elliptical orbit and the inclination of the earth's axis. Mean solar time compensates for the variations in true solar time by averaging out over the year. Greenwich Mean Time (GMT) is a mean solar time.
The true solar time
For the analogous calculation of the true solar time for a day, the time must be noted at a location at which the sun is at its highest point, or passes through the celestial meridian. The time difference between this time and the 12:00 noon local mean time changes over the course of a year. The time difference, or variation within a year, can be observed in the sky as analemma (8).
The digital solar time
The digital solar time is calculated from the Greenwich Mean Time (GMT), or UTC+0, the equation of time and the geographical longitude. The position of a place on the earth can be determined by the geographical longitude and latitude. The television tower on Alexanderplatz in Berlin (Germany) is located at 52.520817° northern latitude and 13.409414° eastern longitude. The longitude is needed to calculate the digital solar time.
Greenwich Mean Time (GMT)
Greenwich Mean Time (GMT) is the mean solar time at the prime meridian (0°) in London, England. Coordinated Universal Time (UTC) is based on Greenwich Mean Time (GMT). Universal Time (UT), on the other hand, is based on true solar time.
Universal Time Coordinated (UTC)
The time in the worldwide time zones, such as Central European Time (CET), which is valid in Central European countries, is coordinated with Greenwich Mean Time (GMT). The initial time for all time zones is called "Coordinated Universal Time" (UTC; English: Coordinated Universal Time; French: Temps universel coordonné).
The 24 time zones on Earth shown on a map.

Graphic: CIA & solar-time.org, public domain.
Time zones and zone time
The Earth is divided into 24 time zones with different zone times. A zone time (English zone time, standard time) is the uniform time in a time zone. The basis of a zone time is the coordinated universal time (UTC) and a longitude of the earth. Central European Time (CET) is aligned with the 15th degree of longitude east (15°E). CET at the 15th meridian of longitude east is exactly one hour from UTC at the prime meridian (0°). Coordinated Universal Time (UTC) is given as UTC+0 for Greenwich Mean Time (GMT) and UTC+1 for Central European Time (CET).
The time zones in Europe shown in a map.

Raw graphic: Rob984 wikimedia (CC BY-SA 4.0)
Criticism of Central European Summer Time (CEST)
The most widespread criticism of Central European Summer Time (CEST) is that, compared to Central European Time (CET), the time in CEST is actually set back one hour, with respect to the fact that people with regular working hours have to go to bed one hour earlier in the evening and get up one hour earlier in the morning. Those who have to go to bed at 23:00 CET and get up at 06:00 in order to get to work rested and on time, have to go to bed at 22:00 CET and get up at 05:00 CET. Of course, in summer it is partly still light at 22:00 and still dark at 05:00, which has an impact on sleep.
For all appointments in CEST, they are always one hour earlier according to CET. You have an appointment at 07:00 in CEST? Then you have the appointment at 06:00 according to CET.
The introduction of CEST had purely economic interests in the European internal market. Health aspects were not taken into account. A time change and the associated shift in bedtime has a negative impact on health. This in turn leads to higher costs for health care and consequently to an economic strengthening of the pharmaceutical industry. Already at the time of the introduction of CEST in Europe (1973 to 1981) Donald Rumsfeld (1975-1977 Secretary of Defense of the USA, 1977-1985 Chairman of the Board of G.D. Searle & Company (introduction of aspartame, from 1985 Monsanto)) warned of the change of danger from the military-industrial complex to the danger from the pharmaceutical-industrial complex. Changes in bedtime mean stress for body and soul and can lead to depression and cancer, where the numbers of people affected are steadily increasing.
Midday sun shift
The digital solar time looks like a gimmick at first glance. But it can also be helpful. In the summer months, some people are advised to avoid the midday sun. Now, Central European Time (CET) deviates very far from true solar time in some locations. Thus, at locations in Germany alone, the midday sun can deviate by up to 1 hour compared to CET.
New Year's Eve & Midnight
The advantage of the digital sundial is that it works even without the sun. Thus, the digital sundial also shows the exact time of midnight. Celebrating the turn of the year on New Year's Eve is possible with the digital sundial in any place in the world according to true solar time (±30 seconds).
Examples:
Central European Time (CET) is 00:06:22 (6 minutes and 22 seconds) different from local mean time at the TV Tower at Alexanderplatz in Berlin. At the TV Tower on Alexanderplatz in Berlin (Germany), midnight (00:00:00) is only 6 minutes and 22 seconds later than CET. Added to this is the difference from true solar time, which fluctuates over a solar year.
At Cologne Cathedral (Germany), Central European Time (CET) differs from local mean time by 00:32:10 (32 minutes and 10 seconds). At Cologne Cathedral, according to mean local time, midnight (00:00:00) is only 32 minutes and 10 seconds later than according to CET. Added to this is the difference from true solar time, which fluctuates over a solar year.
At the beach of Palma de Mallorca (Spain), the Central European Time (CET) differs from the local mean time by 00:49:21 (49 minutes and 21 seconds). At the beach of Palma de Mallorca (Spain), midnight (00:00:00) is 49 minutes and 21 seconds later than CET. Added to this is the difference from true solar time, which fluctuates over a solar year.
The city of Santiago de Compostela in Galicia (Spain) is located west of the prime meridian, i.e. west of Greenwich Mean Time (GMT), but it is not GMT that applies there, but CET. Consequently, the difference between CET and mean local time there is greater than that between CET and GMT. At the Cathedral of Santiago de Compostela in Galicia (Spain), the Central European Time (CET) differs from the mean local time by 01:34:10 (1 hour, 34 minutes and 10 seconds). At the Cathedral of Santiago de Compostela in Galicia (Spain), midnight (00:00:00) is only 1 hour, 34 minutes and 10 seconds later than CET. Added to this is the difference from true solar time, which fluctuates over a solar year.

Nordisk familjebok (1918), runeberg.org, public domain
Note: The times are time-averaged by a few seconds because of elliptical earth's orbit, so that the correlation is easier to recognize.
Stonehenge at winter solstice
Suntime: GMT - 05:30 minutes
Time-equivalence line (Suntime = GMT) at longitude -0.48° (West)
Stonehenge at summer solstice
Suntime: GMT - 09:10 minutes
Time-equivalence line (Suntime = GMT) at longitude 0.43° (East)
Stonehenge
Suntime difference between winter solstice and summer solstice
Suntime at winter solstice + 03:40 compared to suntime at summer solstice
03:40 / 02 = 01:50 minutes
01:50 * 03 = 05:30 minutes
01:50 * 04 = 07:20 minutes
01:50 * 05 = 09:10 minutes
01:50 * 08 = 14:40 minutes
01:50 * 12 = 22:00 minutes
01:50 * 17 = 31:10 minutes
Greenwich at winter solstice
Suntime: GMT + 01:50 minutes
Greenwich at summer solstice
Suntime: GMT - 01:50 minutes
Difference: 03:40 minutes
Stonehenge at vernal equinox
19./20./21. March
Stonehenge Suntime: GMT - 14:40 minutes
Time-equivalence line (Suntime = GMT) at longitude 1.88° (East)
Stonehenge at autumnal equinox
22./23./24. September
Stonehenge Suntime: GMT + 00:00 = time-equivalence (Suntime = GMT)
Time-equivalence line (Suntime = GMT) at longitude -1.82° (West)
Stonehenge is at longitude -1.82°
Greenwich at vernal equinox
19./20./21. March
Greenwich Suntime: GMT - 07:20 minutes
Greenwich at autumnalequinox
22./23./24. September
Greenwich Suntime: GMT + 07:20 minutes
Stonehenge at time-equivalence (Suntime = GMT) in Greenwich
15. April, 13. June, 1. September, 25. December
Suntime: GMT - 07:20 minutes
Stonehenge at Great sun time solstice east
11. February
Time-equivalence line (Suntime = GMT) at longitude 3.56° (East)
Stonehenge Suntime: GMT - 21:30 minutes (+ 00:30 elliptical orbit adjustment = 22:00)
Stonehenge longitude -1.82° (West)
Stonehenge at Great sun time solstice west
03. November
Time-equivalence line (Suntime = GMT) at longitude -4.11° (West)
Stonehenge Suntime: GMT + 09:10 minutes
Stonehenge longitude -1.82° (West)
Stonehenge
Suntime difference between 11. February and 3. November
21:30 + 09:10 = 30:40 minutes (+ 00:30 elliptical orbit adjustment = 31:10)
Stonehenge at Small sun time solstice west
14. May
Time-equivalence line (Suntime = GMT) at longitude -0.92° (West)
Stonehenge Suntime: GMT - 03:40 minutes
Stonehenge longitude -1.82° (West)
Stonehenge at Small sun time solstice east
26. July
Time-equivalence line (Suntime = GMT) at longitude 1.63° (East)
Stonehenge Suntime: GMT - 13:50 minutes
Stonehenge longitude -1.82° (West)
On May 14th, Stonehenge is about twice as far from Greenwich Prime Meridian as the Small sun time solstice west time-equivalence line (local suntime = GMT). The Greenwich Prime Meridian is at the longitude 0°. The time-equivalence line is on May 14th at the longitude -0.91°. Stonehenge is at the longitude -1.82°.
In Stonehenge the time difference between the solstices is 03:40 minutes. Half of it is 01:50 minutes, the double is 07:20 minutes and the quadruple is 14:40 minutes. In Greenwich, at the solstice days, the time difference between local solar time and GMT is 01:50 minutes. In Greenwich, on the day of equinoxes, the time difference between local solar time and GMT is 07:20 minutes. The double is 14:40 minutes. In Stonehenge, on the day of vernal equinox, the time difference between local solar time and GMT is 14:40 minutes. In Stonehenge, on the day of autumnal equinox, the time-equivalence line (Suntime = GMT) is at Stonehenge.